Valve Springs
The purpose of the valve spring is to maintain contact between the components in the valve train, so the valve motion will follow the cam profile. This is most important during the deceleration portion of the cam motion, since the inertia forces in the valve train are opposed to the spring forces. Here we will take the weight or mass of all the valve train components and combine them with the acceleration curve for the cam to calculate the valve train forces. We are assuming the valve train is stiff. Mechanical engineers call this a kinematic analysis of the valve train. This analysis will tell us the absolute minimum spring force that will be required. The valve train is actually not stiff and will vibrate. The vibrations cause periodic fluctuations of the forces, so the actual required spring force will be greater. We consider the more complex case on the Valve Train Dynamics page.
We want to apply Newton's Second Law of motion, i.e. force is equal to mass times acceleration. Here the acceleration is caused by the rotation and profile of the camshaft. The mass is the sum of all the individual components in the valve train. We will first look at a flathead valve train, which is like any direct attack system, e.g. direct OHC. Then we will analyze an overhead valve train with a rocker ratio. A rocker ratio introduces a lever ratio, so equivalent masses are needed to account for this complication. We have done these calculations with an Excel spreadsheet (see Downloads).
The table below contains the weights of the valve train
components in our flathead V8 project. The right columns of
the table list the equivalent weights. The spring has one end that moves with the valve
while the other end is stationery. Intuitively, we would take only half of the springs
weight, but energy conservation considerations suggest that a third
of its weight should be counted. It will not make a big difference
either way. If for no other reason, this analysis is
useful for determining what parts contribute most to the weight of
the system. For example, the Johnson hollow lifters are twice
the weight of a stock Ford lifter.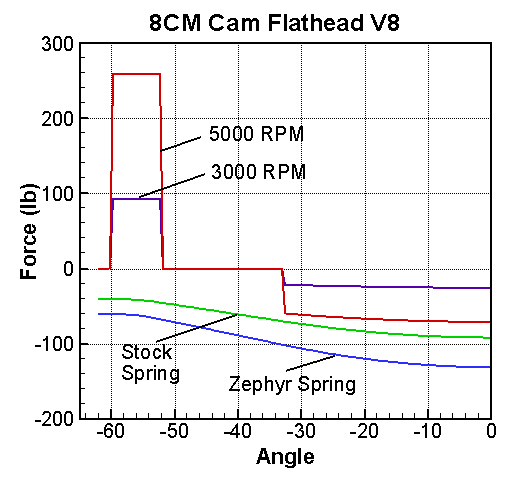
| grams | lb | eqv g | eqv lb | % | |
| lifter, new Johnson hollow | 80.5 | 0.1771 | 80.5 | 0.1771 | 37.4 |
| valve, new 8BA | 96.5 | 0.2123 | 96.5 | 0.2123 | 44.8 |
| retainer, new 8BA | 16.5 | 0.0363 | 16.5 | 0.0363 | 7.7 |
| spring, stock | 65.5 | 0.1441 | 21.8 | 0.0480 | 10.1 |
| total | 215.3 | 0.4737 |
The table gives us the total mass, so if we multiply it by the acceleration rate, we get the inertia forces. We will use the Mercury 8CM cam as an example, since the lift curve is given on the Cam Design page. The acceleration curve is given in (in/deg2). If you multiply the cam rotation rate, in RPM, by 360 degrees per revolution, and divide by 60 (sec/min), you get a rotation rate in (deg/sec). Square this value and multiply it by the acceleration curve to get the acceleration in (in/sec2). The acceleration is then multiplied by the mass from the table and divided by the gravitational conversion, 386.4, to get the inertia forces plotted in the graph at the right. Take note that the inertia forces increase with the square of the engine speed. The acceleration is positive on the flank and negative over the nose. The valve spring must have enough force to counteract the inertia forces on the nose. We have plotted the forces for two different springs: (1) stock springs with 40 lb installed seat force and 160 lb/in spring constant or (2) Zephyr springs with 60 lbs on the seat and 220 lb/in spring constant. The Zephyr springs are actually a bit lighter, but not enough to be significant..
As the rotating speed is increased, the inertia force curve will eventually cross the spring curve, which means the spring is not strong enough to keep the valve train components in contact with each other. According to this analysis, the stock springs are good to about 5400 RPM (engine) and the Zephyr springs are good to 6500 RPM. The analysis says the milder Winfield Semi cam (see Flathead Performance Cams is good to more than 6100 with stock springs and 7400 with Zephyr springs. As stated above, this analysis gives the most optimistic spring performance. Due to vibrations, the springs will not perform this well. It is probably safe to conclude that the Winfield cam needs less spring than a stock 8CM cam, if they are both designed for the same engine speed.
Popular opinion suggests that aftermarket Flathead V8 cams need valve springs that are stiffer than stock springs. Higher engine speeds require stiffer springs, but higher lifts lead to higher spring forces, so weaker springs can be used. We believe that most of the after market cams, like the Winfield cam, have less aggressive profiles than the stock Ford cams (see What is an Aggressive Cam?). This kinematic analysis can help you determine whether you really need stiffer springs for your project. The analysis for our TilTech V8 220 cam gave limits of 5800 RPM for stock springs and 6900 for Zephyr springs. Since we plan to rev this engine more than a stock engine, we've elected to use the stiffer springs.
The analysis for an overhead valve train is more complicated due
to the increased number of components and the rocker arm. We
use the concept of equivalent masses to convert all of the masses to
the cam side of the train. The table below shows the masses
and equivalent masses for the intake of a stock Triumph TR4 valve
train: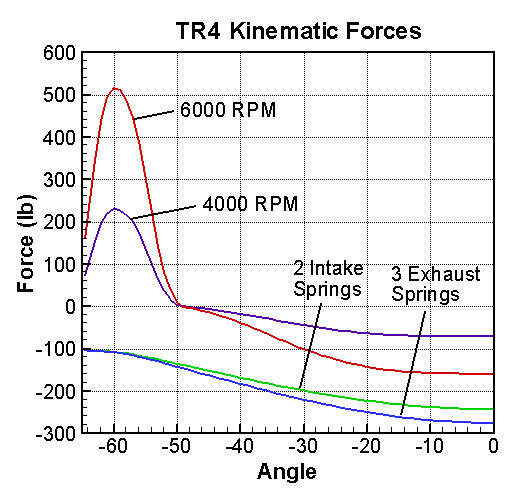
| grams | lb | factor | eqv g | eqv lb | % | |
| Lifter | 70.6 | 0.1556 | 1.000 | 70.6 | 0.1556 | 15.1 |
| Pushrod | 57.7 | 0.1272 | 1.000 | 57.7 | 0.1272 | 12.3 |
| Rocker | 101.0 | 0.2227 | 0.484 | 48.9 | 0.1078 | 10.4 |
| Valve | 72.0 | 0.1587 | 2.205 | 158.8 | 0.3500 | 33.9 |
| Retainer | 27.5 | 0.0606 | 2.205 | 60.6 | 0.1337 | 13.0 |
| Springs (2) | 97.3 | 0.2145 | 0.735 | 71.5 | 0.1577 | 15.3 |
| total | 468.1 | 1.0321 |
The masses on the valve side must be multiplied by the square of the rocker ratio, 1.485. The springs also require the factor of three reduction discussed above. For the rocker ratio, we need its moment of inertia expressed as an equivalent mass. We calculated the factor 0.484 for a TR4 rocker, but typically factors range from 0.5 to 0.7. The rocker ratio really skews the importance of the various components, causing the valve to be dominant. It is not difficult to remove about 10g of material from the lifter or to use aluminum spring retainers that weight 10g less. The concept of equivalent mass makes it easy to evaluate alternatives such as this. The total mass in the table can be combined with theTR4 acceleration curve (top of Cam Design page) to determine the inertia forces shown in the graph at the right.
The Triumph TR4 had a rather advanced spring system for the 1960's. The intake valves used two springs, while the heavier exhaust valves used three. The outer spring was the same in both cases and was wound progressively. According to my measurements it has a spring constant of about 85 lb/in at installed height and 200 lb/in at full valve lift of 0.370 in. For these calculations, we have ignored this complication and used an average spring constant. The values are listed in the table below:
| nominal | factor | equiv. | |
| Intake Seat Force | 70 | 1.485 | 104.0 |
| Intake Spring Const | 252 | 2.205 | 555.7 |
| Exhaust Seat Force | 70 | 1.485 | 104.0 |
| Exhaust Spring Const | 310 | 2.205 | 683.6 |
The table has the composite values for the three exhaust springs and the two intake springs. As with the masses, equivalent values are required to compensate for the rocker ratio. The installed seat force is multiplied by the rocker ratio, while the spring constant is multiplied by the square of the rocker ratio. The spring parameters are combined with the lift curve (top of Cam Design page) to give the spring forces in the graph (upper right). This analysis gives a limiting value of 7400 RPM (engine) before the spring loses its effectiveness. This analysis is highly optimistic for a relatively flexible OHV system. A more accurate Valve Train Dynamic analysis gives a much lower and more realistic limit.
If you would like a copy of the spreadsheet used in these calculations, go to Downloads.